朱茵的脸变成了杨幂

泰勒·斯威夫特一键脱衣，而这一切都是 GAN 做的

2016年人工智能突然爆发，其中的代表概念当然是极其火爆的深度学习。其实深度学习的重要基础概念基本在早期就已经出现了，比如多层神经网络、样本标记、反向传播训练等，都有二三十年的历史了。唯有2014年提出的GAN才算是新鲜事物，被认为是近十年来深度学习领域最有趣的想法。

Nvidia 的 GAN 应用：只需一张照片就能合成视频，让人“动起来”

普通大众听说过GAN的应用，但对其背后的技术原理却了解甚少。深度学习中的常用术语，例如多层神经网络、GPU、权重、训练等，大多数人都比较熟悉。然而，即使是很多理工科的高等教育人士，也不清楚GAN的技术背景和相关术语。

如果你已经对深度学习训练的一般原理有所了解，那么进一步理解 GAN 也并不太难。只需多了解几个概念：生成器、鉴别器，以及两者博弈的纳什均衡即可。

我的经验是，你不需要任何数学公式来理解深度学习，而且 GAN 并不难理解。

本文的目标是帮助普通人理解 GAN 和深度学习的原理，这样当你读到相关文章（比如有哪些新的 GAN 应用）时，会理解得更多。做深度学习或 GAN 开发并不容易，需要学习很多基本操作。这类教程有很多，但理解起来比较困难。

下面我们用一些问答的方式来讲解，目标是解释GAN的工作原理，同时也解释一些深度学习的基础知识。

1. 多层神经网络识别与训练基础知识

你可以快速浏览这一节，而不必关注太多细节。但如果你有兴趣，本文中的一些细节在一般的深度学习科普文章中是没有涉及的。

1. 我知道神经网络通过输入大量标记数据来学习技能。但它们是如何获得这种能力的？它们如何学习？

一般的理解是，一个神经网络中有很多权重系数，这些权重是用有标签的数据进行训练的。然后在应用的时候，用这些权重和输入的图像数据混合进行计算，最后得到一个有意义的输出。理解这个概念就够了。

更深入的理解其实并不难，需要了解多层神经网络的结构，以及基于这个结构的运算过程。

2. 多层神经网络是什么样的？它是如何工作的？

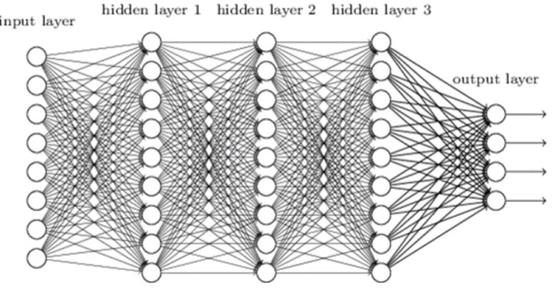
早期的多层神经网络结构

如今的多层神经网络有很多层，比早期的多层神经网络多很多，但是层与层之间的基本关系是一样的。每一层都有很多数据，数据量（维度）是固定的。主要模式是从上一层的数据计算下一层。从上一层到下一层，数据量通常会发生变化，有时减少，有时增加。

数据有两种，一种叫权重，在运算过程中保持不变，常量写在程序里或者预先加载，另一种叫特征值。这就是特征提取的过程，从输入数据开始，在网络的层层变换，直到输出层，呈现出非常明显的特征，连最笨的计算机都能看得出结果。神经网络计算的过程就是不断把计算机无法理解的图像特征，直到连笨计算机都能给出答案的特征。

比如说，人看到一张128*128的图片，会说这张图是猫，那张图是狗，那张图是猪，但是计算机只看到一个128*128的数组，根本不知道是什么。如果最后经过十几层的神经网络变换，通过“特征变换”产生一个3元素的数组（这是猫吗，这是狗吗，这是猪吗），计算机就能看懂了。比如说，如果最后的数组是（1，0，0），计算机会说这张图是猫；如果是（0，1，0），计算机会说这张图是狗；如果是（0，0，0），计算机会说这张图什么都不是；如果是（1，1，0），计算机会说乱七八糟的，根本不知道是什么。总之，计算机会给出一个解释。

当然，实际计算不会这么整齐，通常我们得到的是（猫的置信度，狗的置信度，猪的置信度），比如（0.999，0.100，0.005）。但把这样的小数转换成0和1并不难。

(0, 1, 0) 这个值也有实际用途，在“标注”的时候，它给出了精准的数据。比如我们人工标注了 1000 张图片，标注为猫、狗、猪，其实就是在告诉计算机，给每张图片一个三元素数组 (0, 1, 0)。整个过程中，计算机还是不知道猫、狗、猪是什么，它只知道人给它标注的是 (1, 0, 0)。

3.神经网络如何逐层变换特征？

如果我们想从 128*128 的图像数据中得到三个置信度，一个简单的办法就是，对这 128*128 的值给出三个公式，最终得到三个值。比如，对于一个 128*128 的输入图像矩阵 M，有三个系数矩阵，也就是三个权重矩阵 A、B、C，每个矩阵的大小都是 128*128。对 M 和 A 进行“全乘”操作，也就是将 M 在相应位置的值乘以 A 的权重，再将所有乘数相加，得到一个数 a。再对 M、B、C 进行同样的操作，得到数 b 和 c。这之后，（a,b,c）就是我们最终的特征值。

当然，这种乘法和加法运算得到的数值会非常大，因此要进行“规格化”操作，使其成为0到1之间的小数。

如果我们能巧妙地将ABC三个矩阵的系数对应起来，那么这样做也许会得到有意义的结果。这也是早期神经网络研究的初衷，做一些简单的计算，希望完成任务。的确，一些人工智能任务可以用这种简单的计算过程来解决。比如识别字母和数字0-9和AZ的计算过程，真的就是这么简单。它的输入可能是一张32*32的灰阶图像，最终的输出是（0，0，1，0，…，0）这样的36维数组。

但像猫、狗、猪这样的识别任务就比较复杂了，这个简单的公式确实不行，最后可行的方案是多层神经网络，层数不少。

比如我们要识别一张图片是猫、狗还是猪，输入被处理成标准化的尺寸（比如128*128），这很容易。这是神经网络的第0层，有128*128个“特征值”（或者128*128*3，每个像素有RGB三个值），人眼看到的特征和原图差不多。经过十几层甚至更多的变换，每层的特征值个数就不一样了，比如有的维度是64*64，有的维度是32*32。特征值的维度往往是倍数，大多数时候是缩小一半，有时是扩大一倍。

上一层的特征值结合起来计算下一层的特征值。这基本上就是简单的加法和乘法，先乘后加的“卷积”运算。最常见的是一组 3*3 的 9 个权重，对上一层的特征值进行统一运算。这组 9 个权重被称为“核”或“过滤器”。

以上面的网络结构图为例，我们可以清楚的解释出每一层的特征值是什么样的。

在第0层，输入是320*192的图像（不同大小的原图都被归一化到这个大小），有RGB三个值，所以输入是320*192*3维的数据。

每个过滤器都是3*3的，它会跟320*192矩阵中每一个3*3的区域做“乘加”卷积运算得到一个数。它从左上角开始，然后向右移动一个格子，3*3的区域左边出口会有3个数，右边进入3个新数。它也可以向下移动，每次移动都会跟当前过滤器做一次“乘加”。这样就把320*192个乘数移出去了（其实会少两个，只是把边界填满了）。这样的3*3过滤器用来“卷积”320*192矩阵，得到的矩阵还是320*192。

RGB 有三个矩阵，所以将三个矩阵相加，得到最终的 320*192 矩阵。R、G、B 三个矩阵分别配有一组 16 个 3*3 的滤镜，滤镜总数为 16*3。

第 0 层有 16*3 个 3*3 的滤波器，每个滤波器单独与输入矩阵进行卷积，得到 16 个 320*192 的矩阵作为第 0 层的输出，这也是第 1 层的输入。这一层称为卷积层。

第一层操作比较简单，称为max层。它取矩阵中2*2区域的最大值，将4个数变成一个数。每次操作时，2*2区域“跳”两个格子然后继续。这样，320*192矩阵的大小就变成了160*96。矩阵个数还是16个。通常一个卷积层后面会跟着一个max层。一个操作就是roll一次然后把矩阵大小减半。

第二层是卷积层，有32组3*3的filter，每组16个（对应上一层的16个矩阵），每个filter对一个160*96的矩阵进行卷积，最后16个矩阵加起来就是一个矩阵，32组filter一共是32个矩阵，第三层中的max层将矩阵大小缩小了一半。

这样做完之后，原本 320*192 的图片大小就变成了 40*24。但是图片的数量就变成了 128。人们已经看不懂这些数字到底是什么了，但是从概念上来说，40*24*128 维的数据里就包含了原图的信息。

有时我们会进行上采样，1 变成 4，矩阵就会变成原来的两倍。还有一些其他不同名称的分层运算，但它们都是简单的加、减、乘、除。

最后还有关键的一步，就是把40*24*128的高维数据转化为（0,1,0）的低维数据，依然是先乘以系数再相加，经过十几层滚动之后就是最后一步了。

简单来说，我们从输入矩阵开始，一层一层的计算，这个过程就叫“前向传播”。回过头来看，每一层的输入都是前一层的输出，也就是“特征值”。滤波器就是“权重”，每一层都有很多个权重。滤波器有很多个，每个都是3*3的，有16-128组，每组有16-128个。最终的权重数据文件，小的可以几MB，大的可以几百MB。

如今大量的多层神经网络都是“卷积神经网络”，核心动作就是3*3的滤波器对图像的卷积操作。这种类型的网络之所以在图像识别中非常有用，可以这样理解：3*3的滤波器滚动一个点，会在这个点和周围的8个点之间建立起联系；将图像的宽高减半，再用3*3的滤波器滚动它，会把较远的点与这个点连接起来；对图像尺寸不断减半“下采样”，这样就能让一个点和较远的点产生一些联系，体现在一些权重上；通过训练，就能找到这些近远连接模式，非常有效。

4.什么是“反向传播”训练？

上面的前向传播从图像数据开始，到傻瓜特征值结束，计算过程基本就是乘法加法，但为什么最后能正确识别出猫、狗、猪呢？

其实一开始那些滤波器里面的权重系数都是随机的，最后算出来的傻瓜式的特征值肯定是乱七八糟、完全随机的。比如一张猫的图片，算出来的值是（0.44,0.25,0.66），和正确答案（1,0,0）相差甚远，是完全错误的。

但是深度学习的厉害就在于此，它不怕错，错了还可以训练，我们把那些filter的权重值改一下，让这个计算过程最后输出的值是（1,0,0），怎么改呢？这就是训练的过程。

训练从“误差”开始，比如上例中，误差为（-0.56, 0.25, 0.66），这一层误差出现在最后的输出层。

“反向传播”是指识别时，从输入层到中间层再到输出层进行计算，前一层传递到后一层，特征值发生变化。训练时，将误差作为输入数据，后一层传递到前一层，传递到前一层时，与前一层的输出相比，还有一个误差，根据某一层的误差，改变这一层滤波器的系数，改变滤波器的值。

这种特定的修改非常厉害，是深度学习的核心技术。要先大改后小改，不要改得失控。等学习完所有有标签的样本后，随机权重才会越来越合理。但一次还不够，还是会有很多错误（其实所有样本的误差值总和很大）。

我们反复学习这些样本，上千次，每次都进步一点点，最后总误差就能降低，从最初巨大的总误差值，降低到万分之一，总误差值非常小了，而且我们可以发现，这个神经网络已经学会识别猫、狗、猪了，已经抓住了特征。这时候，哪怕识别不在标注样本里的猫、狗图片，我们还是可以做到的。

其实这个神经网络并不知道自己在做什么，它只是想减少识别样本的误差。

必须强调的是，面对诸多深度学习问题，无论外部应用如何体现，神经网络的本质都是一样的：减少误差。

GAN 中的神经网络结构相同，训练优化目标都是降低误差。不过 GAN 中有两个神经网络：生成器和鉴别器，它们在玩一场博弈。整个框架比单个神经网络有趣得多。

2. GAN 的工作原理

1.GAN如何生成图像？

GAN 训练完成后，作为生成器，也就是上一节介绍的多层神经网络。在应用上，它和识别猫狗的神经网络一样，也是从输入层开始，不断“前向传播”，不过最终输出的是一幅图像。

有时候，输入就是一张图片。比如在照片修复中，输入是一张破损的老照片，GAN 网络根据训练得到的“经验”对老照片进行修复。输入也必须标准化，比如 256*256 的图片大小。生成完成后，生成的图像也是 256*256 的图像，然后再放大回原始照片大小。

有时候，输入可以是随机生成的。比如一个模仿大师画风的应用，一开始会随机生成 256*256 个输入值，肯定乱七八糟。但经过多层神经网络计算后，输出始终带有大师的“特征”。

简单来说，这是一个多层神经网络，输入是一张标准大小的图像数据，经过多层神经网络之后，最终输出的是一张大小相同的图像。在这个过程中，数据的维度可以减半或者翻倍，不断重复。每一层的权重也是一堆3*3的filter，也就是卷积。其实输出和输入就是同样直观的图像数据，比上一节的网络更容易理解。

在实际应用的时候，不需要判别器，事实上，GAN 在实际应用的时候，和一般的深度神经网络架构没什么区别。

GAN真正的本质是训练过程中生成器和鉴别器之间的博弈，没有这场博弈，生成器就无法训练出来。

2. GAN 架构

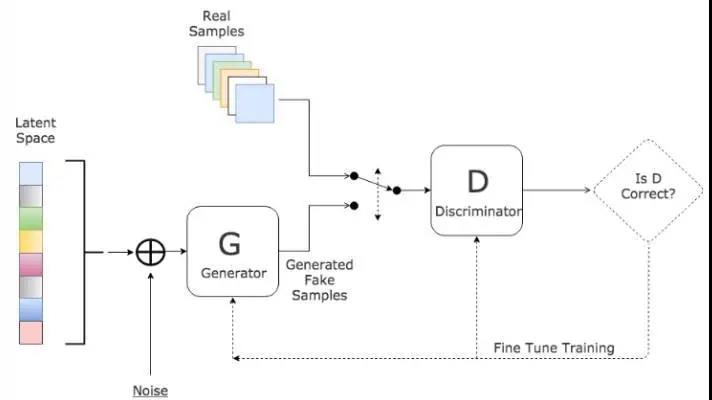
GAN 训练学习架构

上面提到，生成器是一个多层神经网络，输出一张给定大小的图片。鉴别器也是一个多层神经网络，以一张同样大小的图片作为输入，输出一个概率，一个介于 0 和 1 之间的实数。

在整个 GAN 架构中，有一堆“真实的图片”是准备好的样本。这些样本是“无监督的”，不需要人工标注。只要收集一堆图片放在那里就行了。比如说，一堆大师的作品，比如真实的、没有损坏的图片。GAN 的目的就是让生成器生成的东西接近这些真实图片的风格。上一节介绍的猫狗网络是“有监督的”，需要人工标注猫狗图片。

引入判别器是非常巧妙的，它的作用就是判断输入的图像是否真实。一个理想的判别器会对真实图像输出概率1，对生成器生成的图像输出概率0。但是这个判别器并不是把图像和真实图像一个像素一个像素的比较，如果一模一样就为1。它依然遵循一个前向传导的计算过程，从图像输入开始，每一层计算特征值，最后一层输出一个计算值，这个值是一个0~1之间的概率值。

其实判别器本身理解和训练起来并不困难。如果我们准备 10000 张真实图片，随机生成 1000 张假图片，那么数据集就会被自动标注，真的为 1，假的为 0。一开始，判别器里面的权重都是随机生成的，而对这些图片计算出来的权重基本都是错的，都是 0 到 1 之间的小数，比如 0.2、0.7 等等。

然后我们就可以按照上一节的“反向传播”训练过程来训练判别器了。误差就是一张图片上自动标注的0或者1，减去判别器计算出来的0.2或者0.7，就会有一个“误差”。有了误差，我们就可以反向传播，调整判别器网络的系数。经过多张图片、多个batch的学习，判别器就有了一个频谱，对真图片的输出值接近1，对假图片的输出值接近0。只要图片足够多，就能抓住样本的特征。

同一输入图像利用GAN转化为不同的绘画风格：莫奈、梵高、塞尚、浮世绘

相对而言，判别器比较容易训练，而生成器则比较难。就好比我们很容易判断哪幅画是莫奈或者梵高的风格，但我们自己画出来却很难。

GAN 的本质是生成器的训练，通常神经网络的训练都是从网络的输出开始，根据样本的标记值和输出值计算误差反向传播，但在 GAN 架构中，生成器的训练是将生成器和鉴别器连成一个网络！

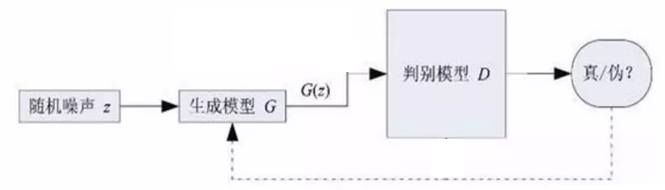
生成器会根据一个随机的输入，生成一张图片，它知道这个图片是假的，但是希望判别器认为它是真的。那么怎么训练它呢？它把生成的图片输入给判别器；判别器会产生一个概率值，说这是它自己的判断，比如说真实的概率是 0.3，而生成器认为目标应该是 1，所以会产生一个 0.7 的误差。这个误差通过判别器传回到生成器的输出层，再传回到生成器内部的各层。在这个反向传播过程中，判别器的权重是不会变的，只是修改了生成器的权重。经过一次训练之后，这个随机输入给判别器的输出就会越来越接近 1。通过重复这样的训练，生成器生成的东西可以让判别器更频繁地输出 1，也就是越来越接近真实的图片。

这个基本的框架就搭建好了，用真实的图片作为引导，训练和引导判别器的“风格品味”，然后用判别器帮助生成器更接近判别器的“风格”，这个过程不需要任何标注。经过足够的训练，生成器生成的图片与真实样本的风格相当接近。人们惊讶地发现，生成器居然学会了模仿大师的画作！

3. 生成器和鉴别器之间的对抗博弈

这个GAN之所以这么巧妙，就是前面说了，把判别器放在生成器后面，帮助生成器训练。从整个框架来看，它更重要的思想是：对抗。

如果我们一开始只是用真实图片和随机的假图片训练一个像样的鉴别器，并且从不改变它，那么这个鉴别器只能帮助生成器训练一次。生成器可以通过少量的训练来学习如何欺骗这个鉴别器。由于鉴别器的系数是固定的，因此欺骗它并不困难。正如一些报道所说，一些神经网络甚至可以在无意义的虫子图片中识别出有意义的东西。

这种欺骗非常糟糕。判别器通过了计算，称生成器生成的一切都是真实的。但在人眼看来，效果很可能非常差，就像虫子图片一样。

那该怎么办呢？很简单，再训练一遍判别器就行了。其实，如果跳出判别器的计算过程，我们可以直接得出结论：只有真实的图片才是真的，其他生成的图片都是假的。我们应该告诉判别器，勇敢地揭穿生成器，你们在造假图片！

因此，判别器会按照“真图输入给 1，假图输入给 0”的原则来调整系数，经过一段时间的训练，它最终会自我调整，对生成器的假图说“不”，理论上，判别器的能力得到了提升。

生成器可以借助“升级后的鉴别器”进行新一轮的训练。

这个过程重复进行，生成器生成的图像越来越逼真，而鉴别器则变得越来越有鉴别力，能够找出生成器生成的图像中的瑕疵。

最后整个过程经过足够多轮之后，理想情况下，生成器的输出和真实图片的风格是完全一致的，判别器会说，我放弃了，你生成的才是真的，我真的看不出来。

GAN 过程的一个常见比喻是造假。造假者和造假者相互竞争，造假者和造假者的技术越来越高超。造假者迫使造假者提高技术，造假者迫使造假者提高技术。最后，造假者获胜，因为也赚到了真金白银。

从博弈论的角度看，生成器和鉴别器在玩一场“零和博弈”：对于同一张图片，一个想当说谎者，另一个想揭穿说谎者，因此总会有一个失败和一个成功。对于生成器的“工作”，如果鉴别器计算接近 1，则生成器成功，对手失败；如果鉴别器计算接近 0，则自己成功，生成器失败。

按照博弈论，这种零和博弈会形成一种“纳什均衡”状态。也就是说，判别器会有一个均衡的输出策略，无论面对什么输入，都会尽量减少自己的损失。这有点难以理解，但却保证了这个框架是合理的，不会出现生成器和判别器之间争吵，生成器的画质来回震荡的情况。

GAN 人脸生成训练失败的产物

在实际训练中，达到这个“纳什均衡”是有些困难的，如果训练不好真的会崩溃，出现各种bug。比如总是生成同一张图（因为这张图保证能通过判别器的检查）；比如生成的人脸有各种缺陷。

理想情况下，训练收敛后，判别器对真实图像输出 0.5，对生成器的假图像输出 0.5，无法再改进。这意味着判别器宣称对手已经毫无瑕疵，自己根本不知道给出的图像是生成的还是真实的。在这种情况下，我采用“给出全部 0.5 概率”的策略。这种策略可以最小化“最大损失”，实现纳什均衡。但这种情况下训练起来也比较困难，生成的图像总会有一些瑕疵。

GAN的思想非常深刻，有人说GAN真正的核心理念是对抗，生成器和判别器的形式完全可以用别的来代替，AlphaGo的升级版Master和AlphaGo Zero就是用了GAN的思想，下棋网络相互竞争，不断变强。

上面介绍了GAN的基本原理，它有很多改进的变体，是深度学习中非常活跃的一个领域，希望上面的基础知识可以帮助大家理解GAN的基本概念。

最后，GAN引入了对抗性学习，但不会取代“非对抗性的深度学习”。目前主要的深度学习应用还是“非对抗性的”，但一些特殊而困难的任务需要引入GAN。

对于一般的深度学习任务，对于“监督学习”来说，有大量的样本很容易标注，只要准备足够多的样本，就能做好，这种开发难度不高，所以被广泛使用。但开发整个GAN框架难度相当大，如果一般任务能通过标注训练解决问题，就没必要强行引入GAN。